• На главную
• О Центре
• Контакты
• Карта сайта
• Расширенный поиск

• Eng
• Rus

• О проекте
• Участники
• Публикации
• Учебные курсы
• Словарь
  терминов
• Часто задаваемые
  вопросы

Мезомасштабные модели гидротермодинамических процессов и переноса антропогенных примесей в атмосфере и гидросфере

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ РАСПРЕДЕЛЕНИЯ ГАЗОВЫХ ПРИМЕСЕЙ И АЭРОЗОЛЕЙ В АТМОСФЕРЕ И НА ПОДСТИЛАЮЩЕЙ ПОВЕРХНОСТИ

А.В. Аргучинцева, В.К. Аргучинцев

Mathematical simulation of climatic distribution of gaseous admixtures and aerosols in atmosphere and on the underlying surface

Arguchintseva A.V., Arguchintsev V.K.

Аннотация

Рассматривается метод математического моделирования распределения атмосферных примесей, основанный на описании региональных климатических характеристик в виде многомерных функций плотностей вероятностей. Приводятся примеры расчетов, оценивающих конкретный вклад промышленных источников в загрязнение атмосферы и подстилающей поверхности.

The method of mathematical simulation of distribution of air pollutant is discussed. The method is based on description of the regional climatic characteristics as many-dimensional functions of probability density. The examples of accounts es-timating the concrete contribution of industrial sources in contamination of an at-mosphere and a spreading surface are reduced.

ВВЕДЕНИЕ

Оценка и контроль загрязнения атмосферного воздуха и подстилающей поверхности в настоящее время основываются как на результатах экспериментального, так и теоретического изучения закономерностей распространения вредных примесей от их источников. Экспериментальные наблюдения за любыми процессами и явлениями дают хорошую диагностику для данной точки наблюдения и в данный момент времени. Но стационарные наблюдения можно организовать лишь в очень ограниченном числе легкодоступных пунктов, а остальные наблюдения (например, экспедиционные) имеют крайне нерегулярный эпизодический характер. Поэтому даже диагностика может быть нерепрезентативна как во времени, так и в пространстве. К тому же наблюдения дают интегральную характеристику, из которой бывает трудно вычленить интересующую исследователя составляющую (например, вклад отдельного предприятия в загрязнение атмосферы). При этом надо отдавать себе отчет, что не всегда наблюдения удается организовать (труднодоступность, дороговизна, отсутствие планируемого объекта), а результат необходимо или желательно уже знать. В этом случае хорошим инструментом являются математические модели, позволяющие проигрывать самые различные ситуации как в диагностическом, так и прогностическом вариантах.

Модель (от французского слова modele) означает образец, воспроизведение какого-либо объекта. Математическая модель – это описание какого-либо класса явлений математической символикой, выраженной в виде уравнения или системы уравнений. Рассматривая изучаемый процесс во времени и в пространстве, мы, как правило, приходим к его описанию в виде дифференциальных уравнений в частных производных.

Различные подходы к математическому моделированию распределения загрязняющих веществ

В настоящее время роль математического моделирования реальных процессов по сравнению с другими методами исследования все более возрастает в связи с широким внедрением мощных компьютеров. Во всех математических моделях переноса и турбулентной диффузии примеси в атмосфере определяющим является дифференциальное уравнение вида:

	(1),

в котором s – концентрация загрязняющей субстанции; x, y, z – оси декартовой прямоугольной системы координат; t – время; u, v, w – составляющие вектора скорости среды (в данном случае ветра) соответственно вдоль осей x, y и z; α - коэффициент неконсервативности примеси; k_x, k_y, k_z – коэффициенты турбулентной диффузии примеси вдоль соответствующих координатных осей; w_g – скорость осаждения примеси на подстилающую поверхность; F(x, y, z, t) – функция, описывающая источники рассматриваемой примеси.

В общем случае коэффициенты обмена в турбулентном потоке представляются тензором второго порядка и записывается матричный оператор, описывающий химические реакции различных субстанций. Уравнение (1) записано в предположении, что оси координат совпадают с главными осями тензора, поэтому недиагональные компоненты тензора исчезают и только диагональные k_xx=k_x, k_yy=k_y, k_zz=k_z отличны от нуля.

В уравнении (1) неизвестными являются s, u, v, w, w_g, α, k_x, k_y, k_z, то есть одно уравнение содержит 9 неизвестных, или говорят, что оно является незамкнутым. Чтобы решить уравнение (1) относительно s , необходимо, во-первых, каким-то образом задать или определить все остальные неизвестные, а во-вторых, поставить начальные (знать начальное состояние процесса) и граничные условия. В зависимости от наличия исходных данных, вида начальных и граничных условий, масштабов решаемой задачи, требований точности, возможных упрощений уравнения (1) возникают и различные подходы к моделированию процессов распространения примесей.

Наиболее сложными в реализации являются модели, когда замыкание уравнения (1) проводится системой дифференциальных уравнений гидротермодинамики [1-3]. Количество замыкающих уравнений может существенно возрастать, если при замыкании мы будем вводить новые факторы, описывающие основные черты атмосферной циркуляции (например, влажность, плотность, давление, температура среды и пр.). Эти модели позволяют детально учесть неоднородность подстилающей поверхности, трансформацию примесей, но очень сложны в реализации. Такие модели реализуются численными методами, сложность которых существенно зависит, например, от аппроксимации производных конечными разностями, выполнения различных критериев для обеспечения вычислительной устойчивости, возможностей вычислительной техники.

Приведем один из результатов численных экспериментов моделирования распределения в приземном слое атмосферы выбросов твердых взвесей на основе уравнений гидротермодинамики и уравнения (1).

Были рассмотрены суммарные выбросы промышленных объектов Приангарья. Изолинии поля рассчитанных приземных концентраций (рис. 1) представлены в долях средней суточной ПДК 0,15 мг/м³. В непосредственной близости от промышленных центров концентрации твердых взвесей в декабре вокруг крупных промышленных центров Приангарья могут достигаться значений 3-5 ПДК. Площади превышения максимальных разовых ПДК (0,5 мг/м³) составляют в Ангарске 150, в Иркутске, Шелехове, Усолье-Сибирском и Черемхове 25 км². Открытая поверхность Байкала загрязняется в основном предприятиями Слюдянки и Байкальска.

Рис.1. Изолинии концентраций твердых взвесей у подстилающей поверхности при типичной ситуации в апреле (шаг - 15 мкг/м³).

Рассмотрим новый подход, развиваемый авторами. Загрязнение окружающей среды отходами промышленных и бытовых предприятий (трубы, стоки, отвалы золы и шлаков и пр.) оказывают на здоровье человека не только прямое, но и косвенное влияние (эрозия почв, поражение флоры и фауны). Самоочищение среды от оказанных на нее вредных воздействий в значительной степени зависит от климатических особенностей местности. По определению А.С. Монина [4] климатом называют статистический ансамбль состояний, проходимых атмосферой за определенный период времени. Необходимо отметить, что наблюдения на гидрометеопостах представляют собой дискретное множество состояний природной среды. В каждый момент времени система находится в одном из этих состояний и с течением времени переходит из одного состояния в другое. Последовательность таких случайных состояний образует полную группу случайных событий (говоря языком вероятности), которую можно рассматривать как марковский процесс без последействия (цепь Маркова). Плотность вероятности перехода из одного состояния в другое для цепи Маркова удовлетворяет интегральному уравнению Смолуховского, решение которого при определенных предположениях относительно вероятностей перехода приводит к решению прямого уравнения Колмогорова [5]. В такой общей постановке задача рассматривается в работе [6].

Однако в целях простоты изложения мы ограничимся рассмотрением лишь некоторых частных случаев, когда решение уравнения (1) сводится к аналитическому. Для этого введем следующие упрощения уравнения (1). Будем считать, что загрязняющая примесь пассивна (движется со скоростью среды и не оказывает на ее скорость какого-либо заметного влияния) и консервативна (не вступает в химические реакции с различными компонентами среды и не переходит из одного химического состояния в другое, то есть коэффициент α=0). Ограничимся рассмотрением установившихся процессов, при которых

Далее ось x ориентируем в направлении ветра, поэтому компонента скорости v=0. Ось z направлена вверх. Вертикальные движения в предположении слабо пересеченной местности малы по сравнению с горизонтальными, поэтому ими можно пренебречь, то есть считать w=0. Для легкой примеси, собственная скорость осаждения которых очень мала, w-w_g=0, для тяжелой - w-w_g=-w_g. Знак минус показывает, что скорость осаждения направлена в противоположную сторону направлению оси z. При наличии ветра можно пренебречь членом, учитывающим диффузию по оси x , поскольку в этом направлении диффузионный поток примеси значительно меньше конвективного [7], то есть считать k_x=0. Тогда исходное уравнение (1) при условии, что источники примеси мы можем учесть в граничных условиях, принимает вид:

(2)

Для легкой примеси, как мы уже говорили, второе слагаемое в левой части уравнения (1) обращается в 0.

Уравнение (2) имеет первый порядок по переменной x и второй – по переменным y и z. Поэтому мы должны поставить одно граничное условие по переменной x и два – по каждой из переменных y и z. Для точечного источника, расположенного в точке с координатами (0,0, H), где H – высота источника, граничное условие запишем в форме:

при

x =0,

где F – масса вещества, выбрасываемая источником в единицу времени, δ - дельта-функция Дирака.

	при		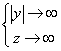и
	при	z = 0.

Последнее граничное условие означает, что средний турбулентный поток примеси у земной поверхности мал, то есть примесь не накапливается на земной поверхности, а с турбулентными вихрями снова уносится в атмосферу. В случае поглощения примеси подстилающей поверхностью (например, водой) граничное условие при z=0 задают в виде s=0.

В общем виде граничное условие при z=0 можно записать в виде:

где β - постоянная, характеризующая взаимодействие примеси с подстилающей поверхностью. В частности, при β=0 и β→∞ имеем два предыдущих условия. Для подстилающих поверхностей вида болот, лесов, лугов значения β определяются, как правило, из опытных данных. Для уравнения (2) при поставленных граничных условиях можно получить аналитические решения соответственно для легкой

	(3)

и тяжелой примеси [7]:

	(4)

где I – функция Бесселя мнимого аргумента; n и m – безразмерные коэффициенты для интерполяции вертикального профиля скорости ветра и коэффициента обмена: u=u₁(z/z₁)ⁿ, k_z=k₁(z/z₁)^m, k_y=k₀u; u₁ и k₁ – соответственно скорость ветра и коэффициент турбулентного обмена по вертикали на высоте z₁; k₀ – константа, зависящая от длины расчетного шага, , m =1.

Или, ограничиваясь первым членом разложения в ряд функции Бесселя, для наземной концентрации имеем:

(4а)

Зная s, можно рассчитать поток взвеси на единицу площади подстилающей поверхности.

Вследствие перегретости примесь в начальной фазе своего распространения обладает восходящей скоростью, но эта начальная фаза непродолжительна, так как под воздействием турбулентности температуры частиц примеси и воздушной среды быстро выравниваются. Точно учесть указанный эффект чрезвычайно трудно, так как пришлось бы решать совместно уравнения диффузии и свободной конвекции частиц газа. Однако даже при значительных перегревах газа этот эффект можно учесть приближенно, заменяя реальный источник примеси геометрической высоты Н фиктивным, несколько приподнятым источником высоты H_e=H+?H.

Существует большое разнообразие полуэмпирических и эмпирических формул, предложенных разными авторами для определения ?H. В нашей стране наиболее приемлемо для нейтральной стратификации атмосферы используется рабочая формула, предложенная М.Е. Берляндом [7]:

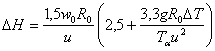
в которой ?H=T_B-T_α; T_B и T_α - соответственно температуры выбросов газа и окружающего воздуха по абсолютной шкале; w₀ – начальная скорость выброса газов; R₀ – радиус устья трубы, g – ускорение свободного падения, u – скорость ветра на высоте флюгера.

Задача замыкается на многолетние данные метеорологических наблюдений стационарных станций и постов, на основе которых строится климатическая функция плотности вероятностей реализации метеокомплексов. При таком подходе многие недостатки аналитических решений, возникающие из-за упрощений исходных дифференциальных уравнений, нивелируются.

В силу того, что записанные аналитические решения (3), (4) и (4а) справедливы для дифференциального уравнения (2), в котором ось абсцисс ориентирована в направлении ветра, расчет примесей в каждой точке пространства приходится вести во вращающейся системе координат, чтобы полностью описать статистическую структуру ветра за рассматриваемый отрезок времени. Если ставится вопрос об оценке накопления тяжелых частиц на подстилающей поверхности, то, как правило, приходится использовать эмпирические законы распределения. Если же необходимо оценить экологическую обстановку с точки зрения вероятности превышения предельно допустимых концентраций, то задачу описания статистической структуры можно свести к теоретическим законам распределения, подобранным из соображений минимальной невязки с реальным эмпирическим распределением. В этом случае время счета значительно сокращается. В качестве таких законов распределения могут выступать нормальный закон распределения, закон Вейбулла и другие. Надо отметить, что идея метода может быть использована и для других типов аналитических решений.

Рассмотрим легкую примесь и оценим частоту превышения некоторых установленных критериев загрязнения за определенный отрезок времени. В качестве таких критериев ограничения концентраций вредных веществ могут выступать, например, предельно допустимые концентрации (ПДК). В нашей стране для населения промышленных районов выделяют два типа ПДК – максимальные разовые и средние суточные. Максимальные разовые ПДК относятся в основном к 20-30-минутному интервалу времени, то есть определяют степень кратковременного воздействия примеси на организм человека без рефлекторных реакций. Значения средних суточных ПДК показывают допустимую степень загрязнения воздуха в течение длительного периода без строгого фиксирования его продолжительности. Средние суточные ПДК, как правило, более жесткие (меньше по величине), чем максимальные разовые. Поэтому области опасных загрязнений для населенных пунктов надежнее определять, ориентируясь на выполнение требований средних суточных ПДК. Надо отметить, что ПДК разработаны для воды, различных видов растительности, почв, особо охраняемых территорий. Значения ПДК, к сожалению, не являются едиными для всех стран и колеблются весьма в широких пределах.

В качестве иллюстраций приведем некоторые результаты расчетных экспериментов.

а) В качестве входной информации в модели рассмотрен многолетний метеорежим по всем стационарным постам г. Иркутска (включая многоуровенные метеоплощадки телевышки) по ежедневным восьмисрочным наблюдениям. Ветровой режим в модели аппроксимировался обобщенным нормальным законом распределения с параметрами, полученными на основе статистической обработки многолетних наблюдений. Наблюдения по высотам на телевышке использовались для определения безразмерного коэффициента n в (3), характеризующего изменение вертикального профиля скорости ветра и горизонтального коэффициента турбулентности степенным законом. Вертикальный коэффициент турбулентности принимался линейно растущим с высотой.

В Иркутске из-за климатических особенностей Восточной Сибири создается высокий потенциал загрязнения атмосферы. Промышленные предприятия размещены в основном в черте города и имеют (примерно 60%) трубы высотою до 30-35 м. Около 200 зарегистрированных высотных источников выбрасывают в атмосферу города окислы азота. Приведем расчеты частоты превышения ПДК=0,04 мг/м 3 в декабре и апреле (рис.2,3). Декабрь выбран как самый неблагоприятный месяц для рассеивания атмосферных примесей в Иркутске, так как характеризуется антициклональным типом погоды, большой повторяемостью штилей, устойчивыми инверсиями. В этом месяце (см. рис.2) опасно загрязнена северо-западная часть города, где концентрации окислов азота могут достигать 10 ПДК в течение 360 ч в месяц. В апреле циклоническая деятельность атмосферы способствует ее очищению, особенно в дневные часы. Однако, несмотря на общее улучшение экологической обстановки в городе, в северо-западной части города до 315 ч в месяц остается превышение 1-2 ПДК (см. рис.3). На указанных рисунках начало координат расположено в центре города. Изолиния 1 оконтуривает область, где превышение указанной нормы происходит с вероятностью, не менее 0,1. Для удобства восприятия вероятность нормирована на количество часов в месяце (вероятности 0,1 соответствует 72 ч).

Рис. 2. Частота превышения ПДК= 0,04 мг/м³ оксида азота (IV) в декабре (Иркутск)

Рис. 3. Частота превышения ПДК=0,04 мг/м³ оксида азота (IV) в апреле (Иркутск)

б) Большие перепады температур вода-суша в районе Байкальского целлюлозно-бумажного комбината (БЦБК) способствуют активному развитию бризовых и горно-долинных циркуляций. Анализ статистической обработки многолетнего метеорологического материала показывает, что преобладающий ветер в осенне-зимний период отклоняется от береговой линии к озеру, а в весенне-летний (период вегетации) – в сторону гор. Был снят рельеф с шагом 1 км на расстоянии 44 км к востоку, 9 км к западу и 15 км к югу от БЦБК. Проведены расчеты опасных зон концентраций для различных ингредиентов. На рисунке 4 приведены модельные расчеты областей превышения 20 ПДК метилмеркаптана (ПДК_мм=9*10^-6) для многолетнего июля. Население в этом летнем месяце дышит повышенными концентрациями дурнопахнущего газа свыше 400 часов. Расчеты, подтвержденные измерениями, показывают, что концентрации ММ в городе могут достигать даже 90 ПДК в течение более 400 ч в месяц.

  Рис. 4. Частота превышения 20 ПДК метилмеркаптана в июле с вероятностью не менее : а - 0,4; б - 0,5; в - 0,6

в) Продемонстрируем модельные расчеты распределения загрязняющих веществ, выбрасываемых в атмосферу источниками Селенгинского целлюлозно-картонного комбината (СЦКК), расположенного на расстоянии около 50 км от Байкала. Анализ результатов статистической обработки климатических ветровых характеристик в районе г. Селенгинска показал, что наиболее опасные зоны загрязнения могут возникать в неблагоприятные месяцы для рассеивания примесей (январь, декабрь – наибольшее распространение примесей в сторону Байкала, ноябрь – наибольшее загрязнение непосредственно в городе). Характер вредных примесей от СЦКК обусловлен принятым на комбинате сульфатным способом производства целлюлозы, приводящим к образованию серосодержащих соединений. Самый высокий уровень из всех выбрасываемых загрязняющих веществ создает метилмеркаптан. Причем над территорией комбината превышения ПДК могут быть 50-100-кратными. На площади около 300 км² превышение 15 значений ПДК возможно до 500 часов в месяц. Границы Байкала достигают не менее 5 значений ПДК. На рисунке 5 приведен расчет частоты превышения 15 ПДК ММ в декабре. Как видим, повышенные концентрации ММ могут достигать почти противоположного берега Байкала.

Рис. 5. Частота превышения 15 ПДК метилмеркаптана в декабре (Селенгинск).

г) Наконец, воспользуемся аналитическим решением (4а) для расчета количества частиц, осаждающихся на подстилающую поверхность за определенный промежуток времени. На рисунке 6 приведены расчеты количества тяжелой примеси, осаждающейся в течение года на акваторию Южного Байкала, Источниками примеси являются все предприятия г. Иркутска. При моделировании учтен дисперсионный состав пылящих частиц, для каждой фракции рассчитана гравитационная скорость.

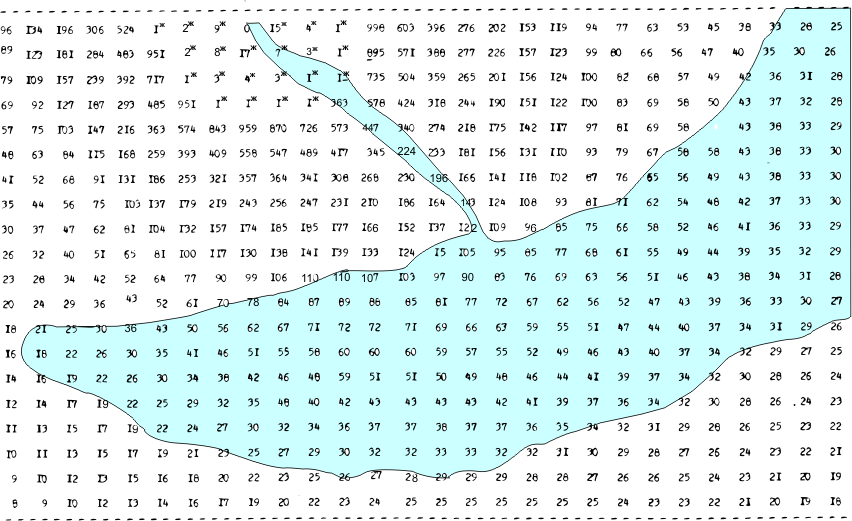
Рис. 6. Накопление (кг/км²) тяжелой примеси в течение года на подстлающей поверхности Южного Прибайкалья от промышленных предприятий г. Иркутска (^ж- порядок числа 10³)

ЗАКЛЮЧЕНИЕ

Рассчитанные с помощью климатической модели характеристики являются интегральными, а потому обладают определенной устойчивостью к отдельным вариациям метеопараметров. Получаемые результаты могут быть использованы различными специалистами: медиками – для анализа причин заболеваемости населения, так как продолжительность (частота) пребывания в опасных зонах концентраций отдельных ингредиентов является критерием неблагоприятного воздействия как на человека, так и на различные биологические системы; дендрологами – для выяснения условий угнетения растительности; хозяйственниками – для оптимального размещения предприятий с точки зрения наименьшей антропогенной нагрузки на экологически значимые районы, изменения режима работы особо загрязняющих предприятий или перевода их на более экологически чистые виды сырья.

ЛИТЕРАТУРА

1. Марчук Г.И., Кондратьев К.Я. Приоритеты глобальной экологии. М.: Наука, 1992. 263 с.
2. Аргучинцева А.В., Аргучинцев В.К., и др. Моделирование и управление процессами регионального развития – М.: Наука, Физматлит, 2001.- 432 с.
3. Аргучинцев В.К., Аргучинцева А.В. Модели и методы для решения задач охраны атмосферы, гидросферы и подстилающей поверхности. - Иркутск: ИГУ, 2001.- 114 с.
4. Монин А.С. Теоретические основы геофизической гидродинамики. Л.: Гидрометеоиздат, 1988. 424 с.
5. Колмогоров А.Н. Об аналитических методах теории вероятностей //Успехи математических наук. М.-Л.: НТЛ, 1938. С. 5-41.
6. Аргучинцева А.В. Моделирование накопления на подстилающей поверхности полидисперсных аэрозолей антропогенного происхождения. 2000. Т.13, №9. С. 865-870.
7. Берлянд М.Е. Прогноз и регулирование загрязнения атмосферы. Л.: Гидрометеоиздат, 1985. 272 с.